Diagnostic Psychometrics
Introductions
W. Jake Thompson
- Ph.D. from KU’s REMS program
- Assistant Director of Psychometrics for Accessible Teaching, Learning, and Assessment Systems
- Research: Applications of diagnostic psychometric models,
- Lead psychometrician and Co-PI for the Dynamic Learnings Maps assessments
- PI for an IES-funded project to develo software for diagnostic models
Conceptual foundations
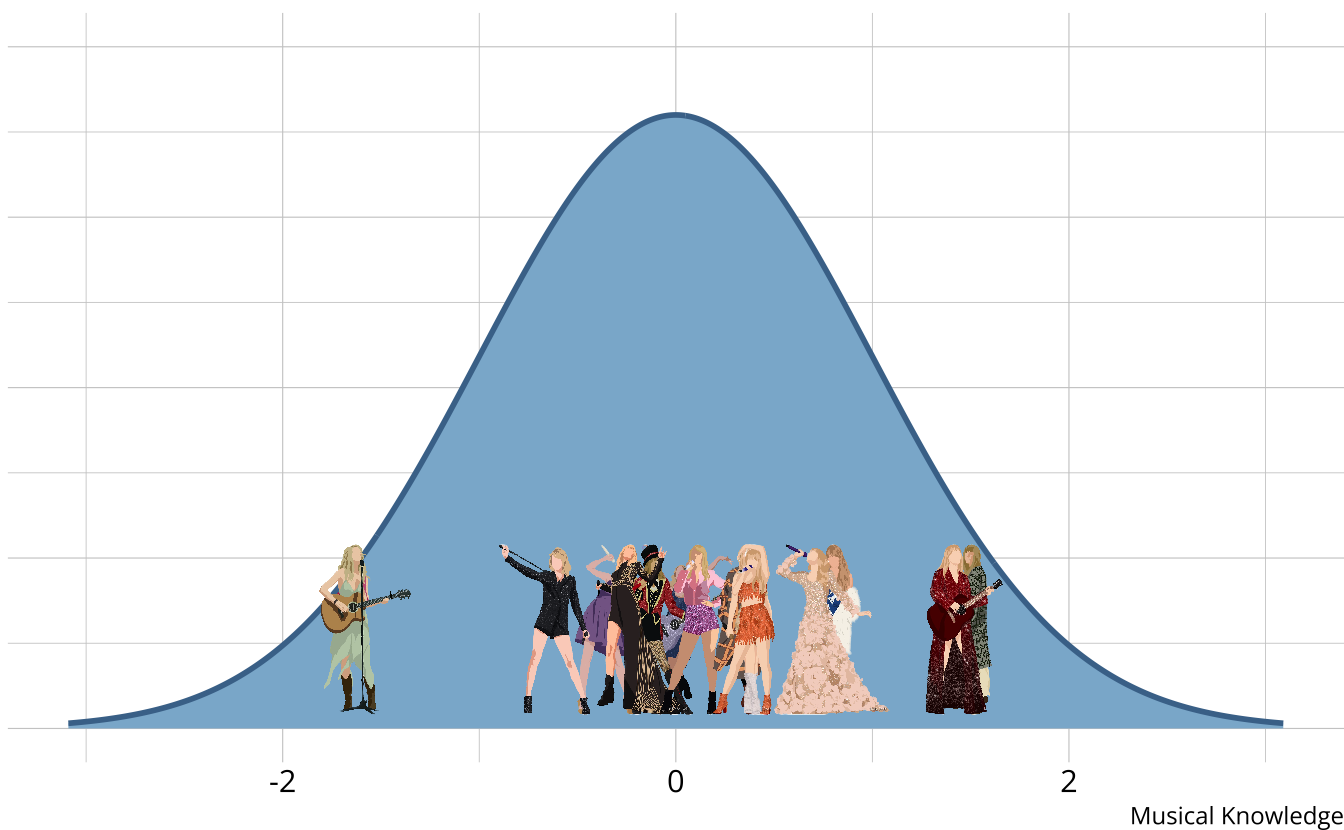
- Traditional assessments and psychometric models measure an overall skill or ability
- Assume a continuous latent trait
Traditional methods
- The output is a weak ordering of teams due to error in estimates
- Confident Red (Taylor’s Version) is the best
- Not confident which is second best (Speak Now (Taylor’s Version), folklore, Lover)
- Limited in the types of questions that can be answered.
- Why is Taylor Swift (debut) so low?
- What aspects do each album demonstrate mastery or competency of?
- How much skill is “enough” to be competent?
Music example
- Rather than measuring overall musical knowledge, we can break music down into set of skills or attributes
- Songwriting
- Production
- Vocals
- Cohesion
- Attributes are categorical, often dichotomous (e.g., proficient vs. non-proficient)
Diagnostic classification models
- DCMs place individuals into groups according to proficiency of multiple attributes
| songwriting | production | vocals | cohesion | |
|---|---|---|---|---|
 |
||||
 |
||||
 |
||||
 |
Answering more questions
- Why is Taylor Swift (debut) so low?
- Subpar songwriting, production, and vocals
- What aspects are albums competent/proficient in?
- DCMs provide classifications directly
Diagnostic psychometrics
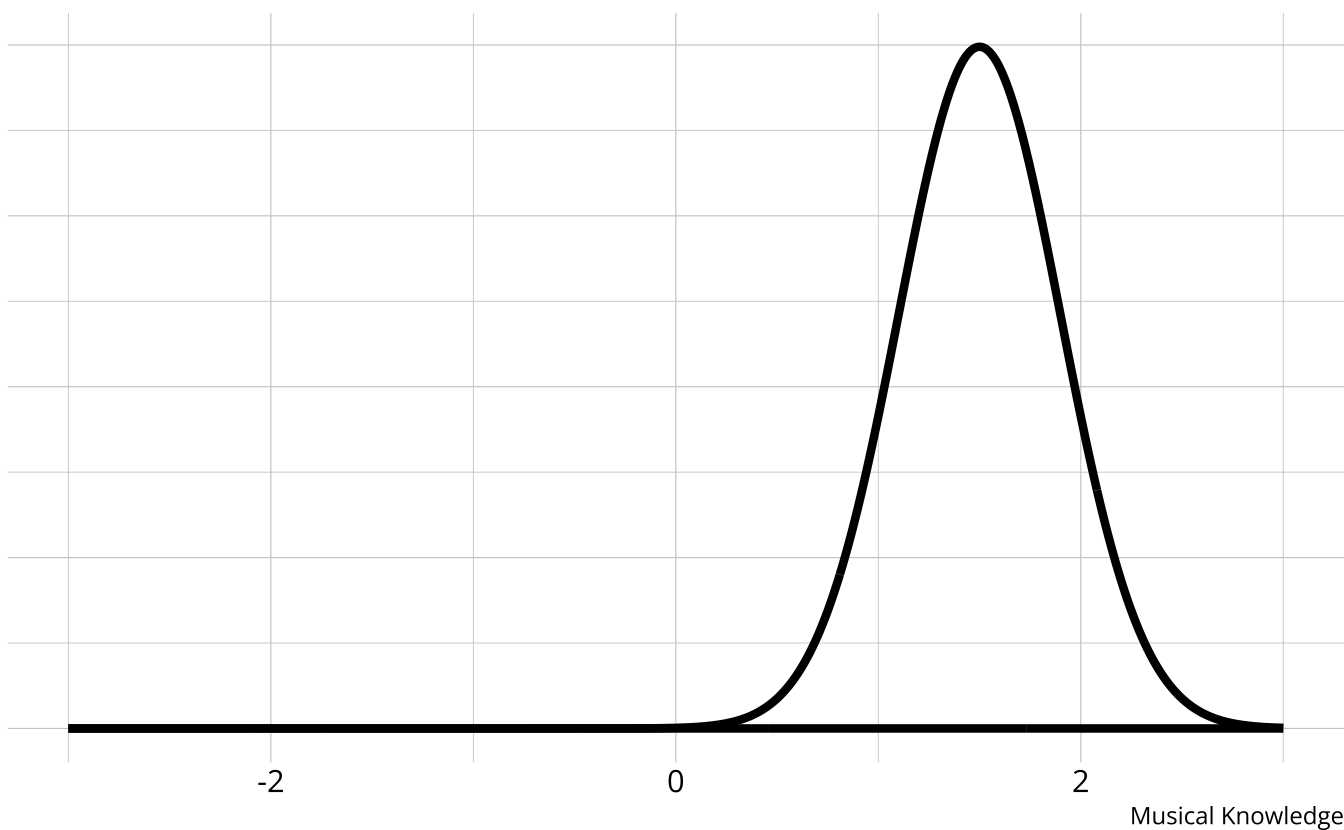
- Designed to be multidimensional
- No continuum of student achievement
- Categorical constructs
- Usually binary (e.g., master/nonmaster, proficient/not proficient)
- Several different names in the literature
- Diagnostic classification models (DCMs)
- Cognitive diagnostic models (CDMs)
- Skills assessment models
- Latent response models
- Restricted latent class models
Benefits of DCMs
- Fine-grained, multidimensional results
- Incorporates complex item structures
- High reliability with fewer items
Results from DCM-based assessments
| songwriting | production | vocals | cohesion | |
|---|---|---|---|---|
|
||||
 |
||||
 |
||||
 |
||||
|
||||
 |
||||
 |
||||
|
||||
 |
||||
 |
||||
|
||||
 |
||||
 |
||||
 |
- No scale, no overall “ability”
- Students are probabilistically placed into classes
- Classes are represented by skill profiles
- Feedback on specific skills as defined by the cognitive theory and test design
Item structures for DCMs
Item structure: Which skills are measured by each item?
- Simple structure: Item measures a single skill
- Complex structure: Item measures 2+ skills
Defined by Q-matrix
Interactions between attributes when an item measures multiple skills driven by cognitive theory and/or empirical evidence
- Can proficiency of one skill compensate for non-proficiency of another?
- Are skill acquired in a particular order (e.g., hierarchy)?
| item | songwriting | production | vocals | cohesion |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 |
| 2 | 1 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 1 |
| 4 | 0 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 0 | 1 |
| 7 | 1 | 0 | 0 | 0 |
| 8 | 1 | 0 | 1 | 0 |
| 9 | 0 | 0 | 1 | 0 |
| 10 | 0 | 1 | 1 | 0 |
| 11 | 1 | 0 | 1 | 0 |
| 12 | 0 | 0 | 0 | 1 |
| 13 | 0 | 0 | 1 | 0 |
| 14 | 1 | 0 | 0 | 0 |
| 15 | 0 | 1 | 0 | 0 |
| 16 | 1 | 1 | 0 | 0 |
| 17 | 0 | 0 | 1 | 1 |
| 18 | 0 | 0 | 0 | 1 |
| 19 | 0 | 1 | 0 | 0 |
| 20 | 0 | 0 | 1 | 1 |
| 21 | 0 | 1 | 0 | 0 |
| 22 | 1 | 0 | 0 | 0 |
| 23 | 0 | 0 | 0 | 1 |
| 24 | 0 | 0 | 1 | 0 |
| 25 | 0 | 0 | 1 | 1 |
| 26 | 0 | 1 | 1 | 0 |
| 27 | 0 | 0 | 1 | 0 |
| 28 | 1 | 1 | 0 | 0 |
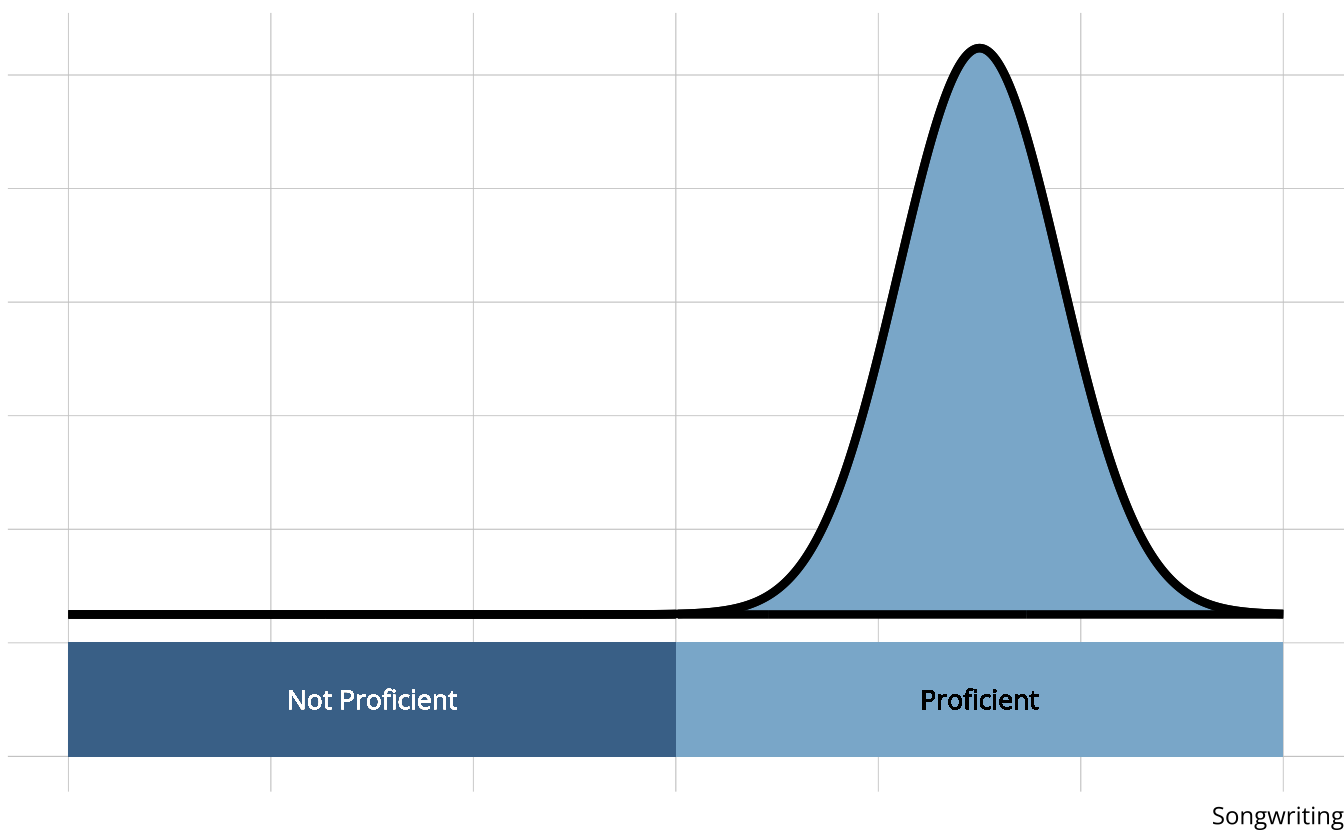
Classification reliability
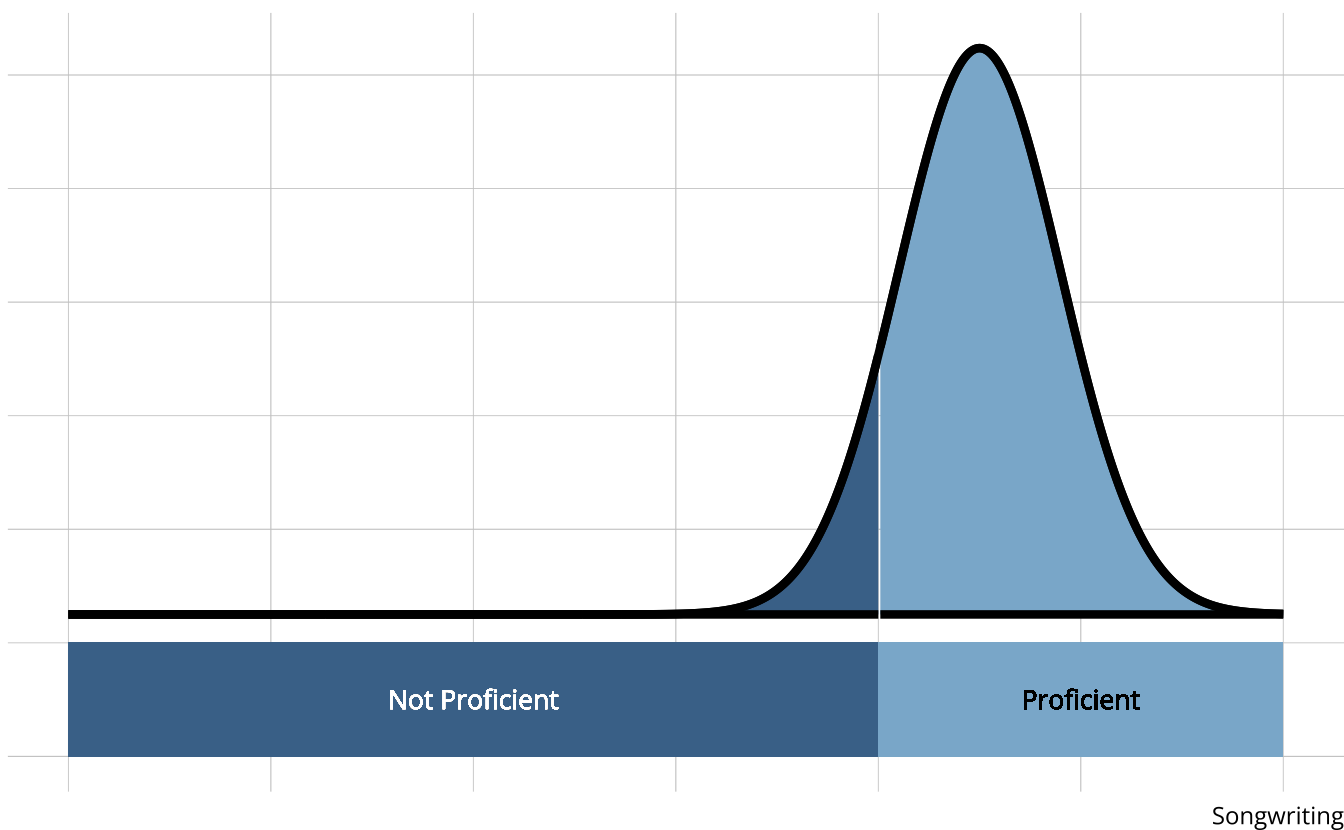
- Easier to categorize than place along a continuum
- Can set a proficiency threshold to optimize Type 1 or Type 2 errors
When are DCMs appropriate?
Success depends on:
- Domain definitions
- What are the attributes we’re trying to measure?
- Are the attributes measurable (e.g., with assessment items)?
- Alignment of purpose between assessment and model
- Is classification the purpose?
Example applications
- Educational measurement: The competencies that student is or is not proficient in
- Latent knowledge, skills, or understandings
- Used for tailored instruction and remediation
- Psychiatric assessment: The DSM criteria that an individual meets
- Broader diagnosis of a disorder
When are DCMs not appropriate?
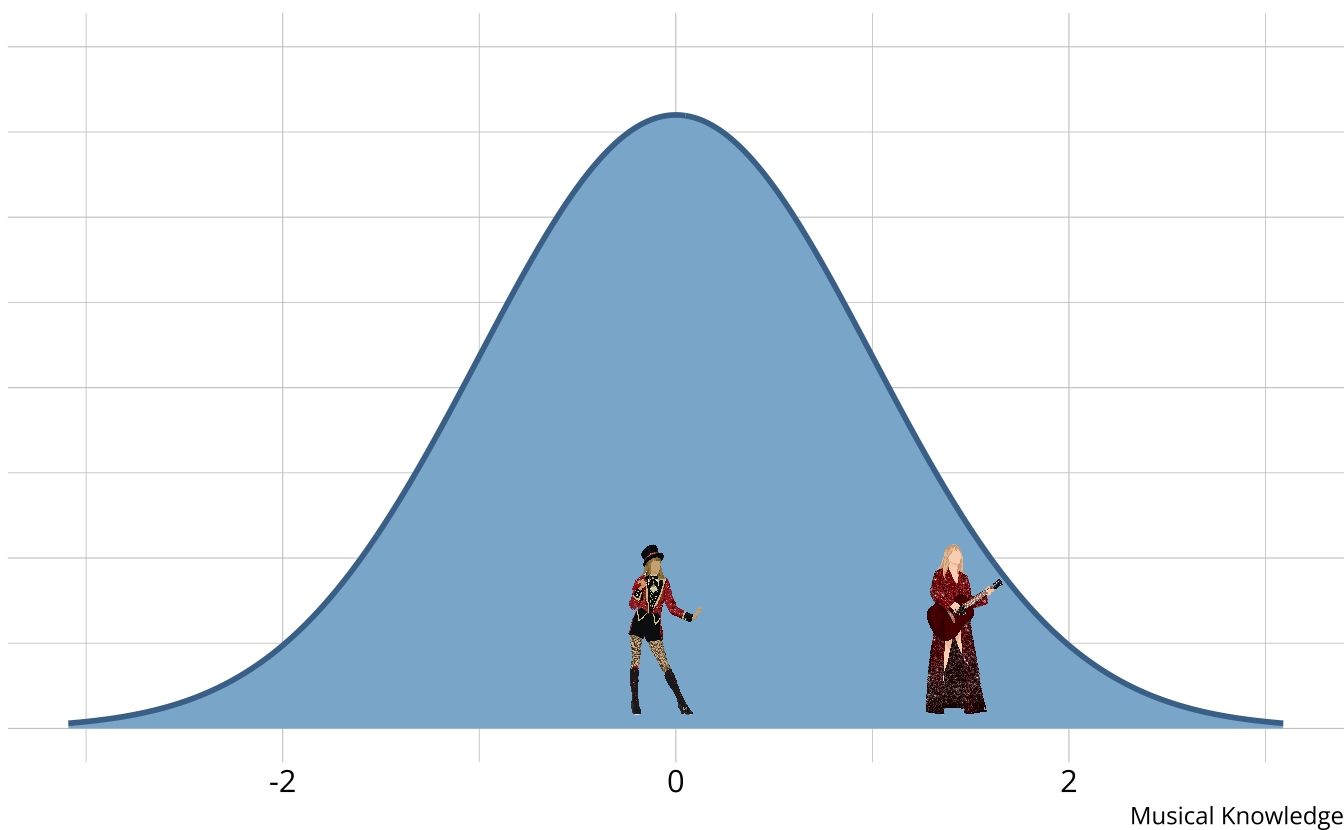
When the goal is to place individuals on a scale
DCMs do not distinguish within classes
| songwriting | production | vocals | cohesion | |
|---|---|---|---|---|
|
||||
|
Conceptual foundation summary
- DCMs are psychometric models designed to classify
- We can define our attributes in any way that we choose
- Items depend on the attribute definitions
- Classifications are probabilistic
- Takes fewer items to classify than to rank/scale
- DCMs provide valuable information with more feasible data demands than other psychometric models
- Higher reliability than IRT/MIRT models
- Naturally accommodates multidimensionality
- Complex item structures possible
- Criterion-referenced interpretations
- Alignment of assessment goals and psychometric model
Statistical foundations
DCMs as statistical models
Latent class models use responses to probabilistically place individuals into latent classes
DCMs are confirmatory latent class models
- Latent classes specified a priori as attribute profiles
- Q-matrx specifies item-attribute structure
- Person parameters are attribute proficiency probabilities
Terminology
Respondents (r): The individuals from whom behavioral data are collected
- For today, this is dichotomous assessment item responses
- Not limited to only item responses in practice
Items (i): Assessment questions used to classify/diagnose respondents
Attributes (a): Unobserved latent categorical characteristics underlying the behaviors (i.e., diagnostic status)
- Latent variables
Diagnostic Assessment: The method used to elicit behavioral data
Attribute profiles
With binary attributes, there are 2A possible profiles
Example 2-attribute assessment:
[0, 0]
[1, 0]
[0, 1]
[1, 1]
DCMs as latent class models
P(Xr=xr)=C∑c=1νcI∏i=1πxiric(1−πic)1−xir
Observed data: Probability of observing examinee r's item reponses
Structural component: Proportion of examinees in each class
Measurement component: Product of item response probabilities
Measurement models
- Traditional psychometrics: Item response theory, classical test theory
- A single, unidimensional construct
- Student results estimated on a continuum
- Performance on individual items determined by an “item characteristic curve”
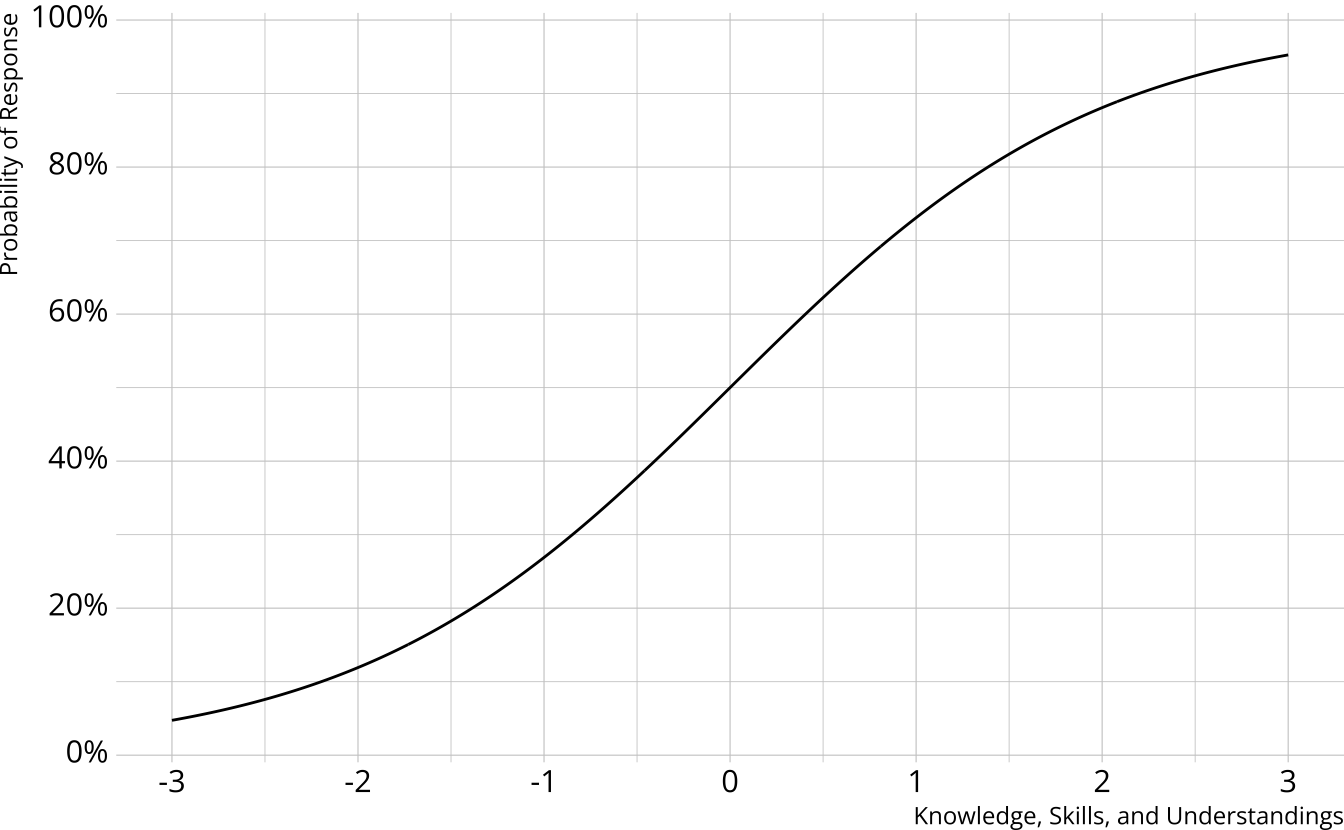
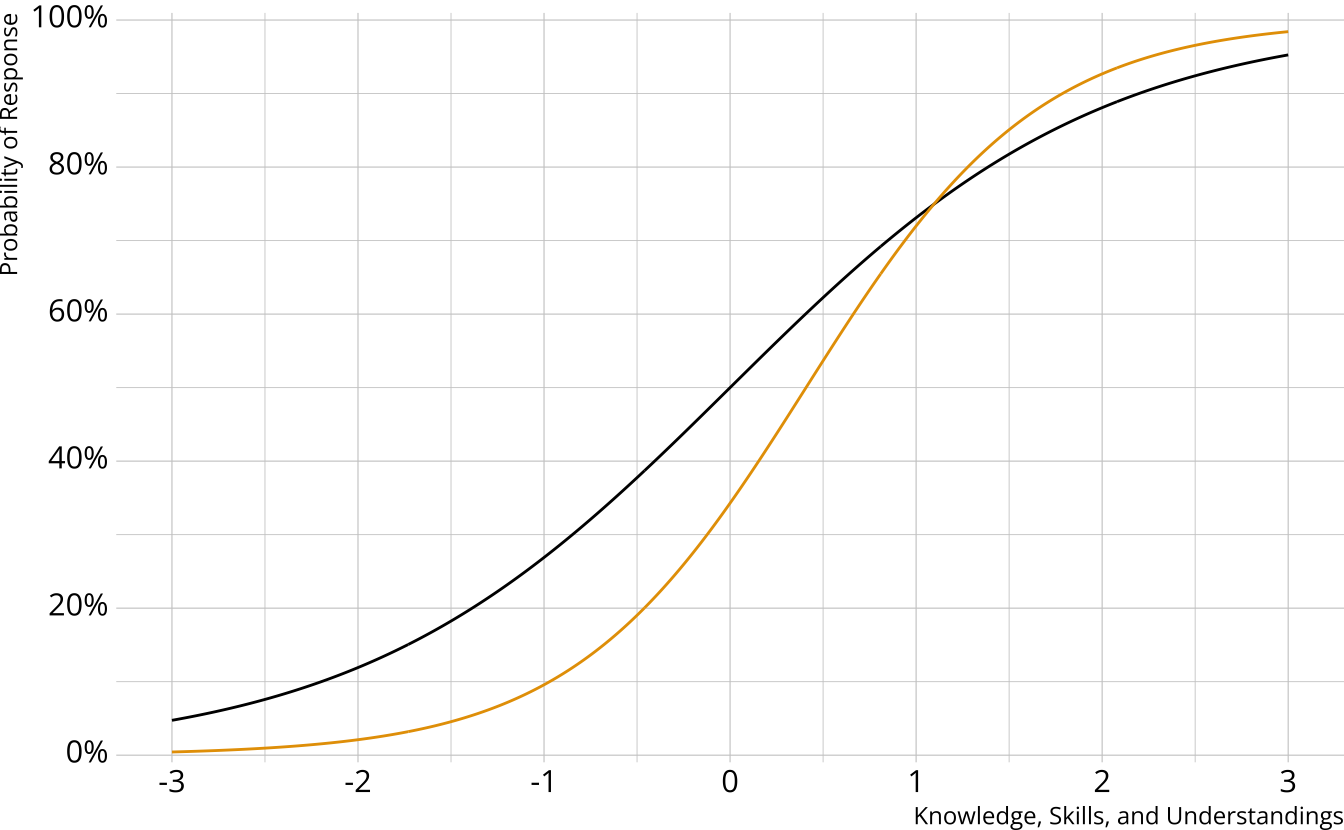
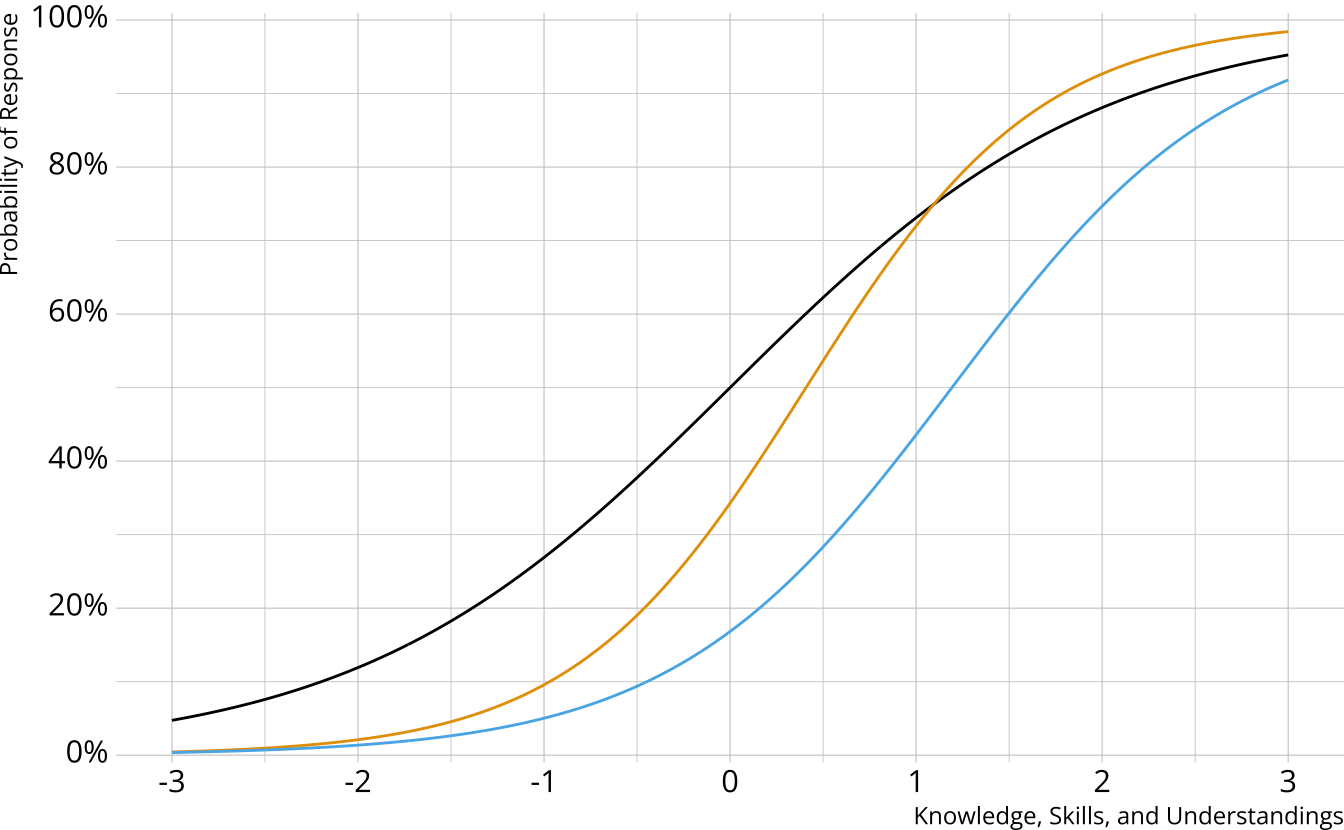
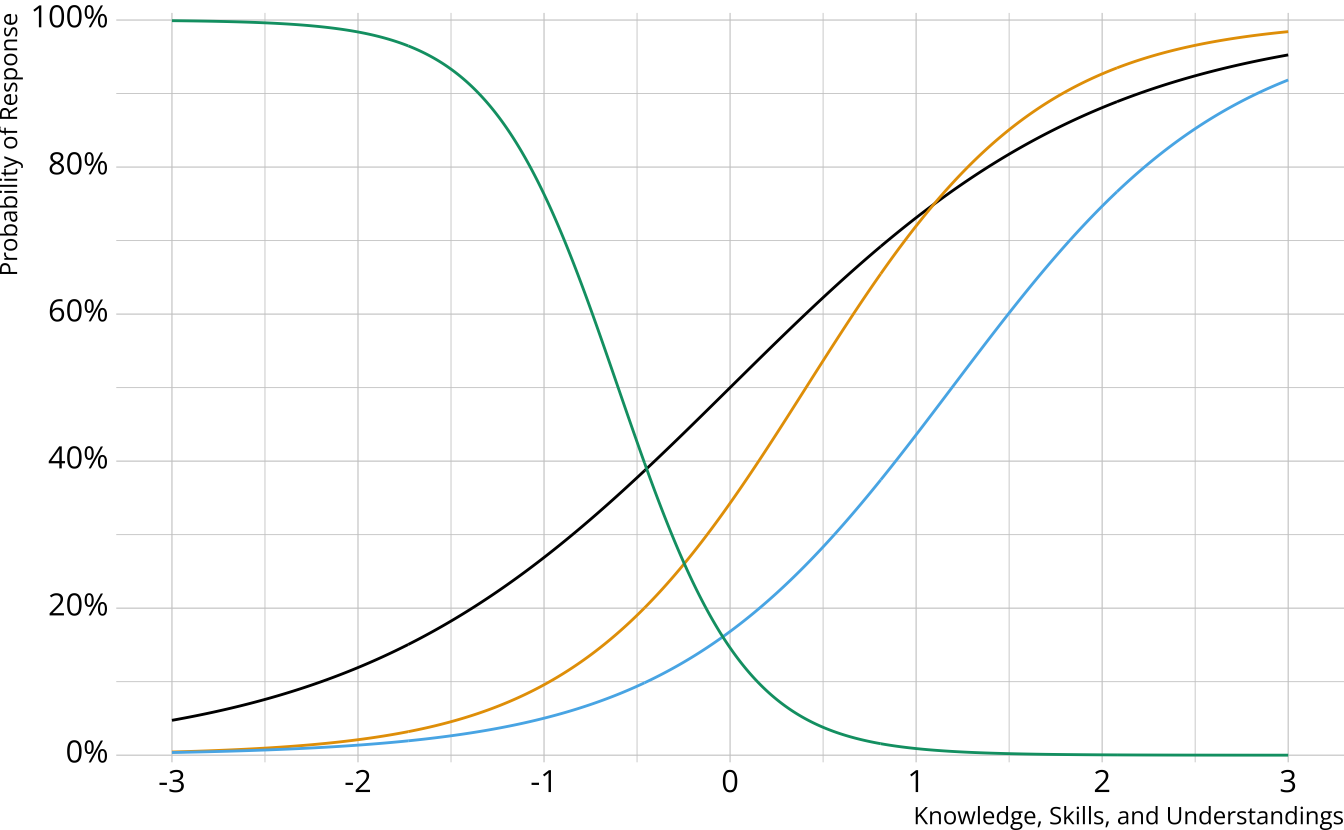
Diagnostic assessment items
Can be multidimensional
No continuum of student achievement
Categorical constructs
- Usually binary (e.g., master/nonmaster, proficient/not proficient)
DCM measurement models
Reminder: We’re currently focusing on the measurement model.
P(Xr=xr)=C∑c=1νcI∏i=1πxiric(1−πic)1−xir
Different DCMs define πic in different ways
DCM measurement models
Consider an assessment that measures 2 attributes
With binary attributes there are 2A possible profiles
[0, 0]
[1, 0]
[0, 1]
[1, 1]
Items can measure one or both attributes
Item characteristic bar charts
Single-attribute DCM item
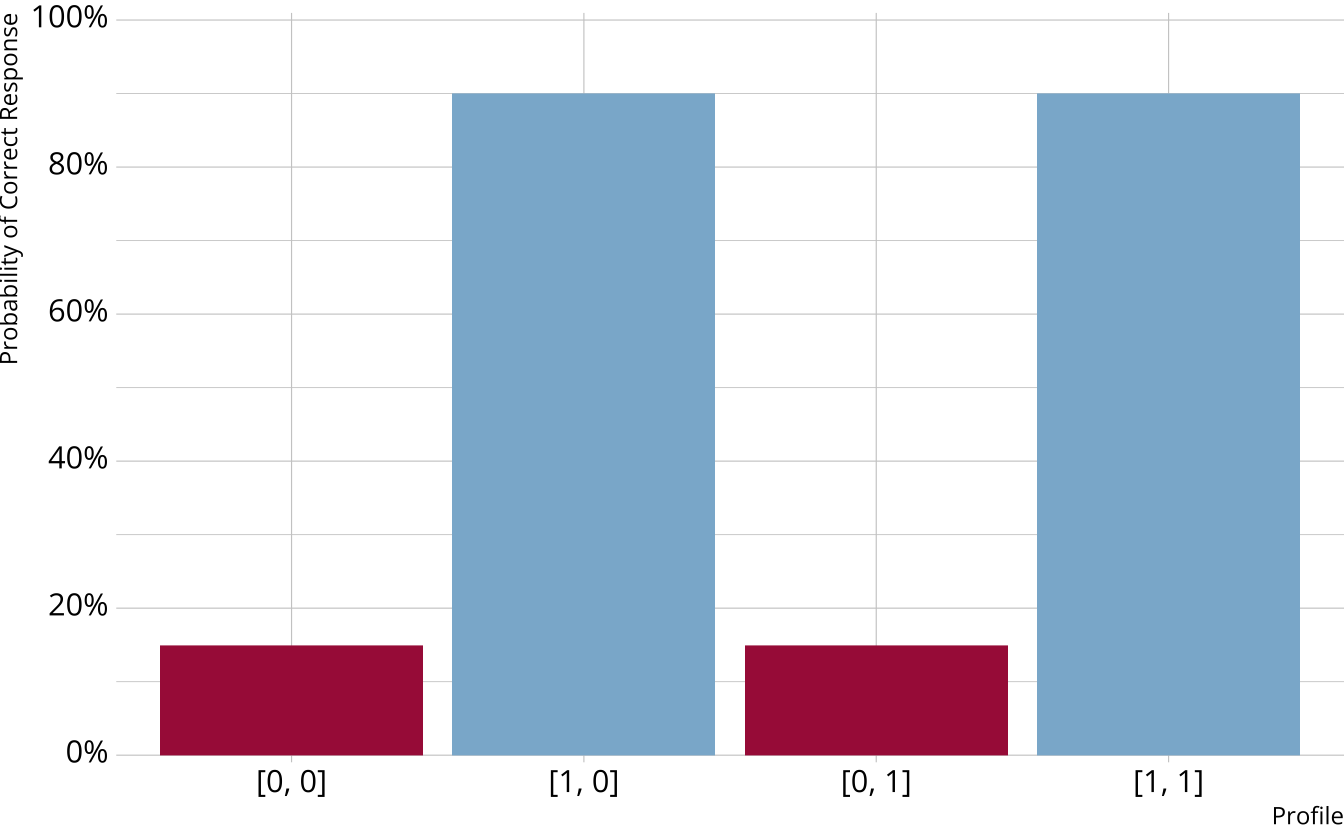
Multi-attribute items
When items measure multiple attributes, what level of mastery is needed in order to provide a correct response?
Many different types of DCMs that define this probability differently
- Compensatory (e.g., DINO)
- Noncompensatory (e.g., DINA)
- Partially compensatory (e.g., C-RUM)
General diagnostic models (e.g., LCDM)
Each DCM makes different assumptions about how attributes proficiencies combine/interact to produce an item response
Compensatory DCMs
Must be proficient in at least 1 attribute measured by the item to provide a correct response
Deterministic inputs, noisy “or” gate (DINO; Templin & Henson, 2006)
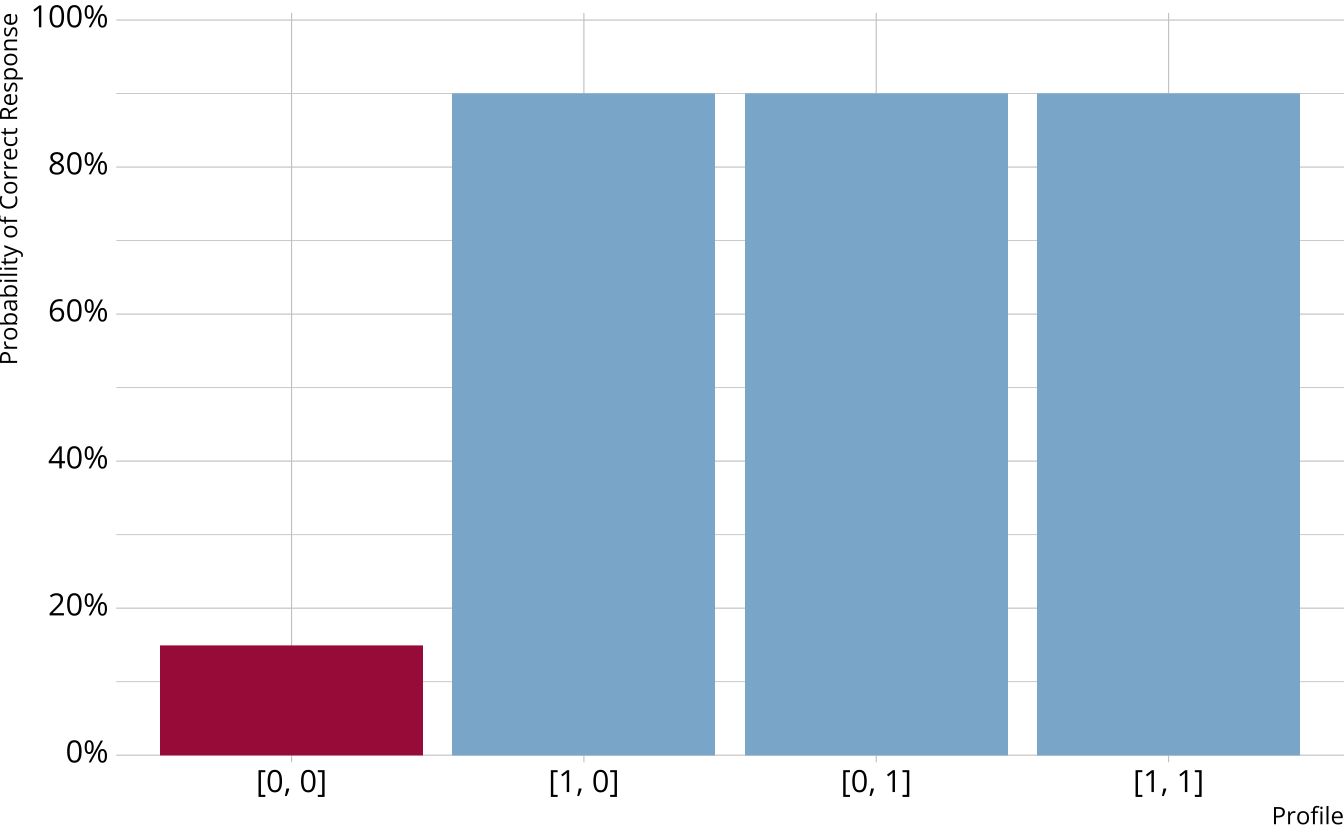
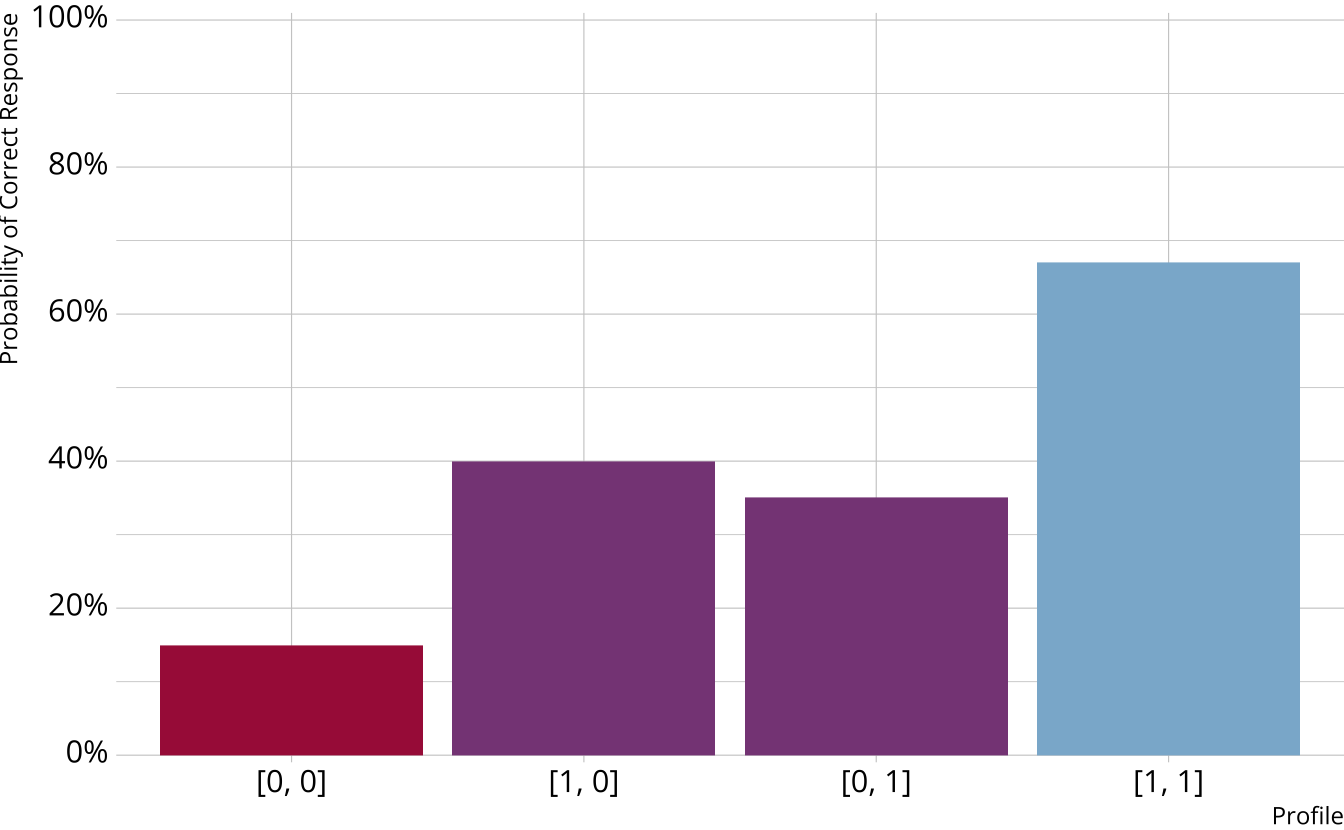
Non-compensatory DCMs
Must be proficient in all attributes measured by the item to provide a correct response
Deterministic inputs, noisy “and” gate (DINA; de la Torre & Douglas, 2004)
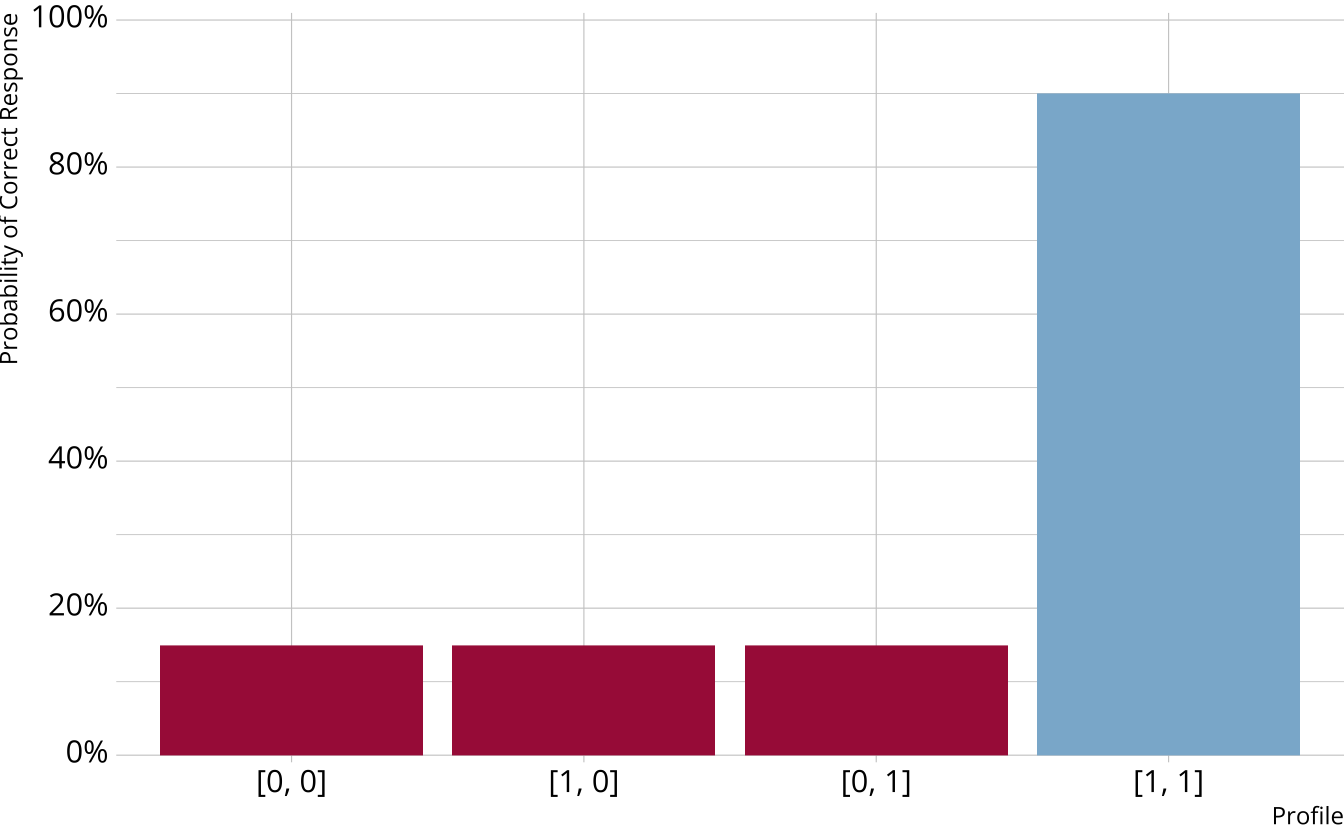
Partially Compensatory DCMs
Separate increases for each acquired attribute
Compensatory reparameterized unified model (C-RUM; Hartz, 2002)
Which DCM to use?
DINO, DINA, and C-RUM are just 3 of the MANY models that are available
Each model comes with its own set of restrictions, and we typically have to specify a single model that is used for all items (software constraint)
General form diagnostic models
- Flexible; can subsume other more restrictive models
- Again, several possibilities (e.g., G-DINA, GDM)
- Loglinear cognitive diagnostic model
Loglinear cognitive diagnostic model (LCDM)
Different response probabilities for each class (partially compensatory)
Log-linear cognitive diagnostic model (LCDM; Henson et al., 2009)
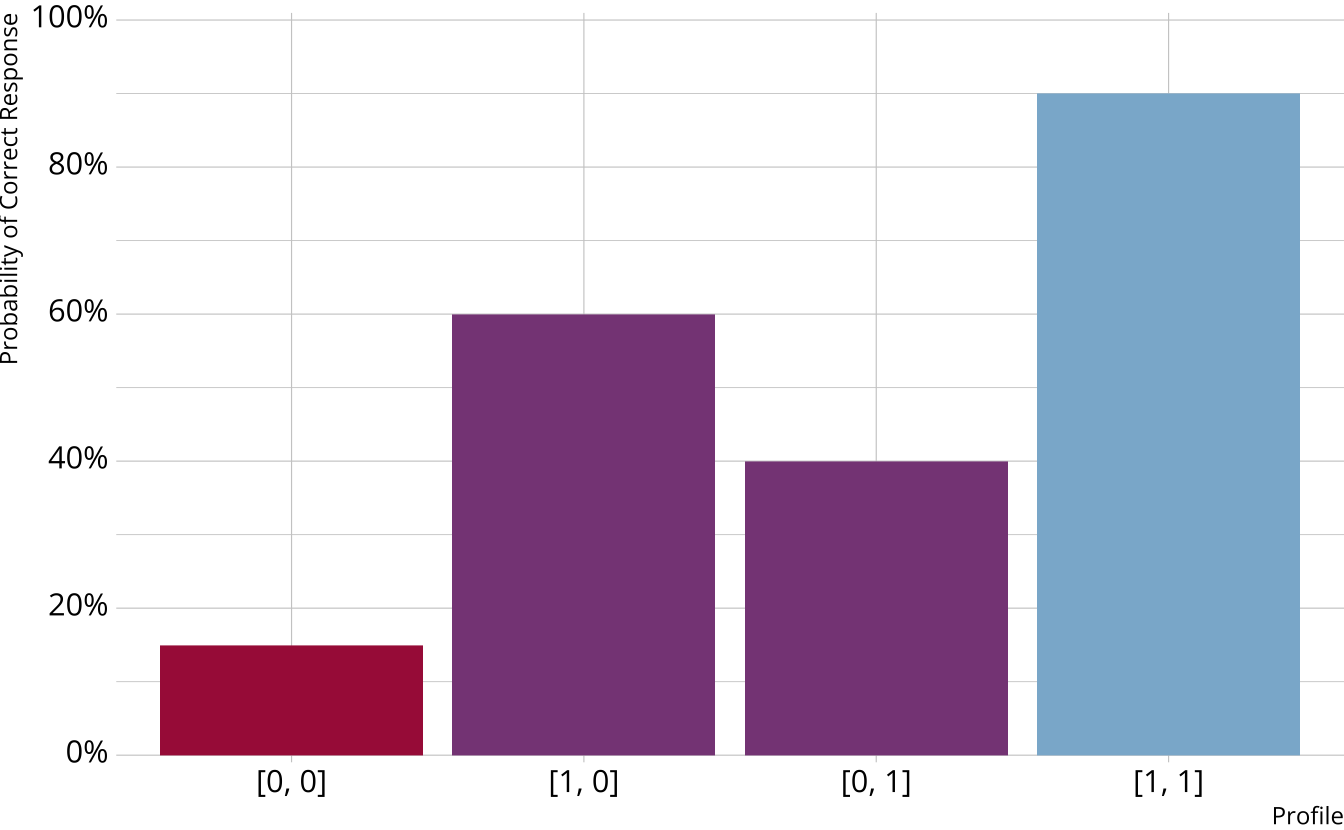
Simple structure LCDM
Item measures only 1 attribute
logit(Xi=1)=λi,0+λi,1(1)α
λi,0: Log-odds when not proficient
λi,1(1): Increase in log-odds when proficient
α: Attribute proficiency status (either 0 or 1)
Subscript notation
- i = The item to which the parameter belongs
- e = The level of the effect
- 0 = intercept
- 1 = main effect
- 2 = two-way interaction
- 3 = three-way interaction
- Etc.
- (α1,…) = The attributes to which the effect applies
- The same number of attributes as listed in subscript 2
Complex structure LCDM
Item measures multiple attributes
logit(Xi=1)=λi,0+λi,1(1)α1+λi,1(2)α2+λi,2(1,2)α1α2
Log-odds when proficient in neither attribute
Increase in log-odds when proficient in attribute 1
Increase in log-odds when proficient in attribute 2
Change in log-odds when proficient in both attributes
Defining DCM structures
Attribute and item relationships are defined in the Q-matrix
Q-matrix
- I × A matrix
- 0 = Attribute is not measured by the item
- 1 = Attribute is measured by the item
The LCDM as a general DCM
So called “general” DCM because the LCDM subsumes other DCMs
Constraints on item parameters make LCDM equivalent to other DCMs (e.g., DINA and DINO)
- Interactive Shiny app: https://atlas-aai.shinyapps.io/dcm-probs/
- DINA
- Only the intercept and highest-order interaction are non-0
- DINO
- All main effects are equal
- All two-way interactions are -1 × main effect
- All three-way interactions are -1 × two-way interaction (i.e., equal to main effects)
- Etc.
- C-RUM
- Only the intercept and main effects are non-0 (i.e., interactions are not estimated)
Testable hypotheses!
Estimation and Evaluation
Model Estimation
What is measr?
- R package that provides a fully Bayesian estimation of DCMs using Stan
- Provides additional functions to automate the evaluation of DCMs
- Model fit
- Classification accuracy and consistency
Example data
- Simulated data: https://bit.ly/sp24-epsy896-dcm
# A tibble: 500 × 29
album `1` `2` `3` `4` `5` `6` `7` `8` `9` `10` `11` `12`
<chr> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int> <int>
1 Melo… 0 1 1 1 0 1 0 0 1 1 0 0
2 A Ni… 1 0 0 0 0 0 0 0 0 0 0 0
3 Cann… 1 0 0 0 0 0 1 0 0 0 0 0
4 BORN… 1 0 0 1 1 0 0 0 1 0 0 0
5 Loose 1 0 0 1 1 1 0 0 0 1 1 1
6 Red 0 1 0 0 1 1 0 1 0 0 1 0
7 Wild… 0 0 1 1 0 0 0 0 1 0 0 1
8 Dawn… 0 0 1 1 0 1 0 1 0 0 0 0
9 than… 0 0 0 0 0 0 0 0 1 1 0 1
10 In A… 1 0 1 1 0 1 1 0 0 0 0 0
# ℹ 490 more rows
# ℹ 16 more variables: `13` <int>, `14` <int>, `15` <int>, `16` <int>,
# `17` <int>, `18` <int>, `19` <int>, `20` <int>, `21` <int>, `22` <int>,
# `23` <int>, `24` <int>, `25` <int>, `26` <int>, `27` <int>, `28` <int>measr_dcm()
Estimate a DCM with Stan
ts_dcm <- measr_dcm(
1 data = ts_dat, qmatrix = ts_qmat,
resp_id = "album",
2 type = "lcdm",
3 method = "mcmc", backend = "cmdstanr",
4 iter_warmup = 1500, iter_sampling = 500,
chains = 4, parallel_chains = 4,
5 file = "fits/taylor-lcdm"
)- 1
- Specify your data, Q-matrix, and ID columns
- 2
- Choose the DCM to estimate (e.g., LCDM, DINA, etc.)
- 3
- Choose the estimation engine
- 4
- Pass additional arguments to rstan or cmdstanr
- 5
- Save the model to save time in the future
measr_dcm() options
type: Declare the type of DCM to estimate. Currently supports LCDM, DINA, DINO, and C-RUMmethod: How to estimate the model. To sample, use “mcmc”. To use Stan’s optimizer, use “optim”backend: Which engine to use, either “rstan” or “cmdstanr”...: Additional arguments that are passed to, depending on themethodandbackend:rstan::sampling()rstan::optimizing()cmdstanr::sample()cmdstanr::optimize()
View predictions
- Two types of results
- Class-level results
- Attribute-level results
# A tibble: 500 × 17
album `[0,0,0,0]` `[1,0,0,0]` `[0,1,0,0]`
<fct> <rvar[1d]> <rvar[1d]> <rvar[1d]>
1 Melodrama 1.1e-06 ± 1.2e-06 1.3e-08 ± 1.4e-08 3.7e-05 ± 3.0e-05
2 A Night At The Oper… 9.5e-01 ± 2.3e-02 8.5e-03 ± 5.1e-03 8.5e-03 ± 5.3e-03
3 Cannibal (Expanded … 1.2e-02 ± 9.4e-03 4.2e-03 ± 3.4e-03 9.1e-01 ± 4.7e-02
4 BORN PINK 1.5e-01 ± 7.1e-02 1.6e-04 ± 1.2e-04 3.1e-01 ± 1.2e-01
5 Loose 8.5e-06 ± 9.6e-06 5.1e-08 ± 6.1e-08 1.5e-04 ± 1.2e-04
6 Red 1.8e-03 ± 1.9e-03 1.4e-02 ± 1.2e-02 9.7e-02 ± 6.2e-02
7 Wildfire 1.7e-04 ± 1.5e-04 1.6e-07 ± 1.7e-07 1.4e-03 ± 1.3e-03
8 Dawn FM 5.4e-05 ± 6.1e-05 2.6e-07 ± 2.8e-07 1.2e-03 ± 7.5e-04
9 thank u, next 7.1e-02 ± 4.9e-02 5.8e-06 ± 4.9e-06 3.7e-02 ± 2.5e-02
10 In A Perfect World … 1.2e-08 ± 1.6e-08 7.1e-05 ± 5.7e-05 9.8e-07 ± 8.7e-07
# ℹ 490 more rows
# ℹ 13 more variables: `[0,0,1,0]` <rvar[1d]>, `[0,0,0,1]` <rvar[1d]>,
# `[1,1,0,0]` <rvar[1d]>, `[1,0,1,0]` <rvar[1d]>, `[1,0,0,1]` <rvar[1d]>,
# `[0,1,1,0]` <rvar[1d]>, `[0,1,0,1]` <rvar[1d]>, `[0,0,1,1]` <rvar[1d]>,
# `[1,1,1,0]` <rvar[1d]>, `[1,1,0,1]` <rvar[1d]>, `[1,0,1,1]` <rvar[1d]>,
# `[0,1,1,1]` <rvar[1d]>, `[1,1,1,1]` <rvar[1d]># A tibble: 500 × 5
album songwriting production vocals
<fct> <rvar[1d]> <rvar[1d]> <rvar[1d]>
1 Melodrama 0.000419 ± 0.000278 0.9422 ± 0.0340 0.966461 ± 0.019196
2 A Night At The Op… 0.008565 ± 0.005107 0.0086 ± 0.0053 0.033112 ± 0.019671
3 Cannibal (Expande… 0.080788 ± 0.044734 0.9842 ± 0.0114 0.000045 ± 0.000039
4 BORN PINK 0.000471 ± 0.000233 0.3845 ± 0.1307 0.508834 ± 0.137168
5 Loose 0.001590 ± 0.001057 0.8967 ± 0.0614 0.935788 ± 0.042500
6 Red 0.746107 ± 0.099693 0.6544 ± 0.1407 0.703408 ± 0.128450
7 Wildfire 0.000059 ± 0.000035 0.1359 ± 0.1027 0.951212 ± 0.028540
8 Dawn FM 0.000650 ± 0.000407 0.9544 ± 0.0313 0.003481 ± 0.003005
9 thank u, next 0.000020 ± 0.000010 0.2147 ± 0.0833 0.890630 ± 0.065815
10 In A Perfect Worl… 0.997949 ± 0.001355 0.9638 ± 0.0216 0.004456 ± 0.004106
# ℹ 490 more rows
# ℹ 1 more variable: cohesion <rvar[1d]># A tibble: 14 × 5
album songwriting production vocals
<fct> <rvar[1d]> <rvar[1d]> <rvar[1d]>
1 Red 0.746107 ± 0.099693 0.6544 ± 0.14069 0.70341 ± 0.12845
2 Fearless (Taylor's… 0.915897 ± 0.058410 0.0308 ± 0.02352 0.02697 ± 0.01902
3 Speak Now (Taylor'… 0.999783 ± 0.000145 0.2619 ± 0.12795 0.12060 ± 0.07406
4 Midnights 0.997510 ± 0.001928 0.0206 ± 0.01822 0.86307 ± 0.09284
5 reputation 0.561946 ± 0.157150 0.0631 ± 0.04698 0.95791 ± 0.02410
6 Red (Taylor's Vers… 0.999976 ± 0.000017 0.9808 ± 0.01220 0.97884 ± 0.01149
7 Fearless 0.527831 ± 0.173573 0.0092 ± 0.00751 0.00091 ± 0.00068
8 1989 (Taylor's Ver… 0.195956 ± 0.116831 0.9960 ± 0.00250 0.99601 ± 0.00216
9 Taylor Swift 0.000055 ± 0.000031 0.0012 ± 0.00073 0.00011 ± 0.00008
10 folklore 0.999904 ± 0.000074 0.9855 ± 0.01114 0.99407 ± 0.00352
11 Speak Now 0.575813 ± 0.147118 0.3276 ± 0.13558 0.00072 ± 0.00052
12 evermore 0.826752 ± 0.077166 0.9304 ± 0.04031 0.91412 ± 0.04216
13 Lover 0.494974 ± 0.152578 0.0016 ± 0.00140 0.89823 ± 0.06781
14 1989 0.000043 ± 0.000025 0.9465 ± 0.03016 0.84713 ± 0.07194
# ℹ 1 more variable: cohesion <rvar[1d]>Model Evaluation
How to evaluate DCMs?
- Three types of model evaluation we’ll discuss:
- Absolute model fit
- Relative model fit
- Reliability
Absolute fit
How well does the model fit the data?
Overall model fit
- M2 (Liu et al., 2016)
- Posterior predictive model checks (PPMCs; Thompson, 2019)
Item-level fit
- PPMCs (Sinharay & Almond, 2007)
M2
- For the M2 statistic, p-values greater than .05 indicate acceptable fit
# A tibble: 1 × 8
m2 df pval rmsea ci_lower ci_upper `90% CI` srmsr
<dbl> <int> <dbl> <dbl> <dbl> <dbl> <chr> <dbl>
1 310. 309 0.478 0.00218 0 0.0173 [0, 0.0173] 0.0371- The
fit_m2()function also returns some other model fit statistics that may be familiar- RMSEA: root mean square error of approximation
- SRMSR: standardized root mean square residual
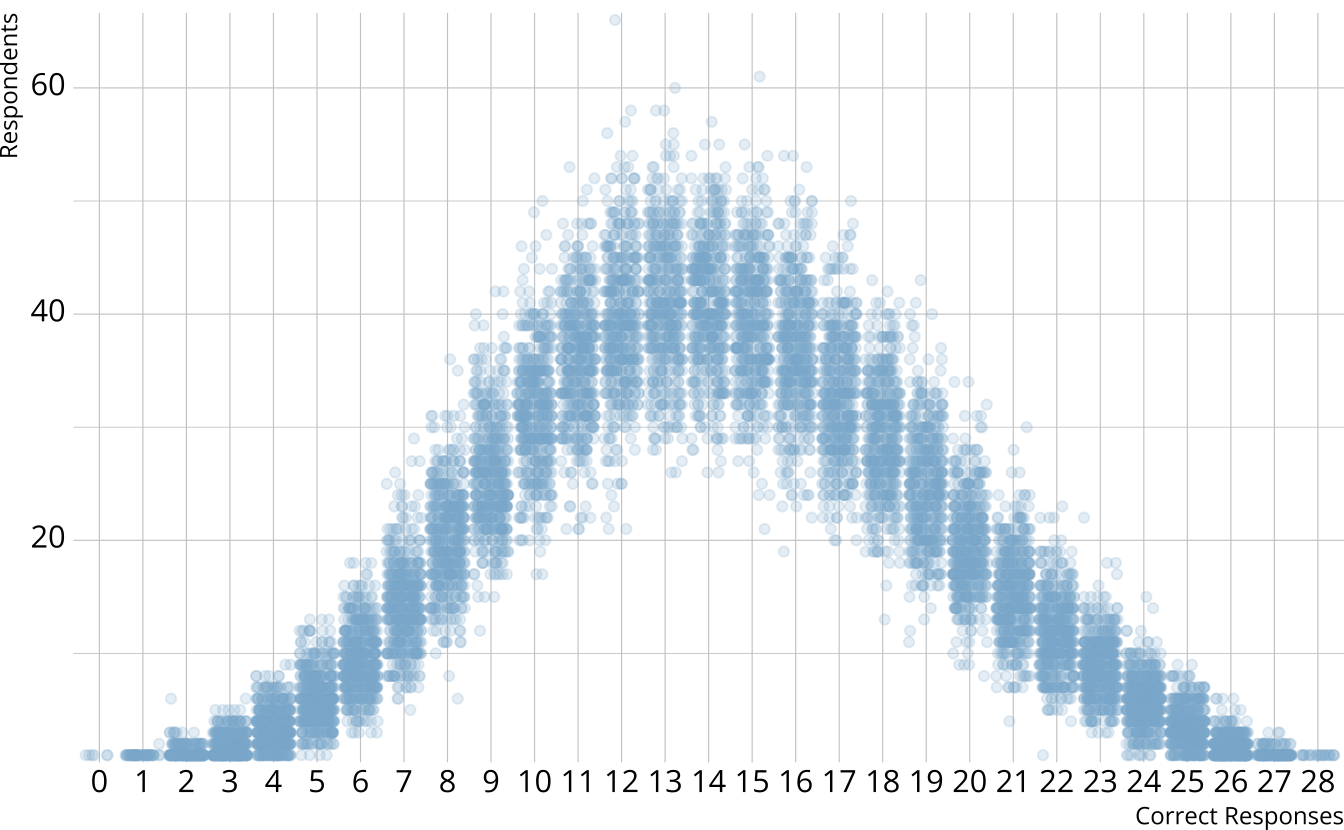
PPMC: Raw score distribution
- For each iteration, calculate the total number of respondents at each score point
- Calculate the expected number of respondents at each score point
- Calculate the observed number of respondents at each score point
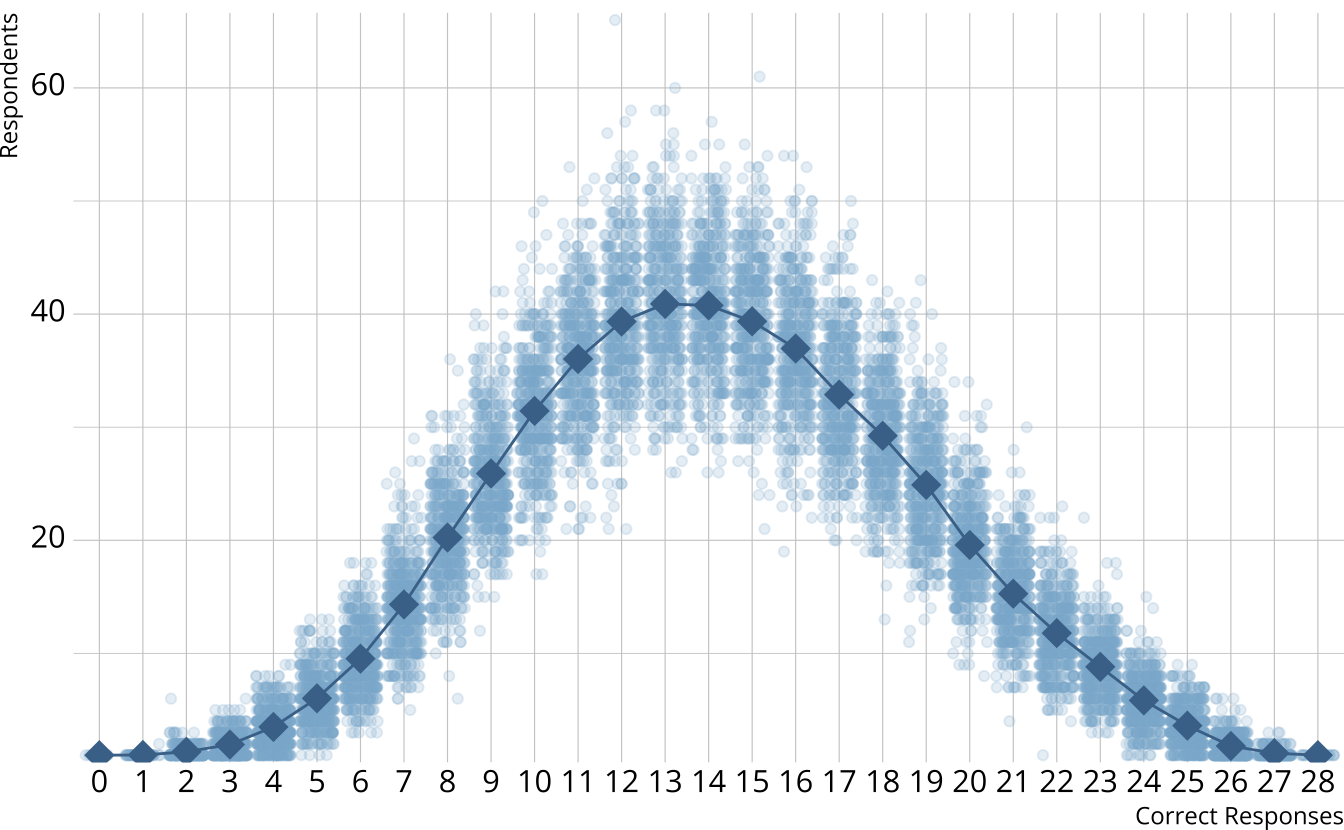
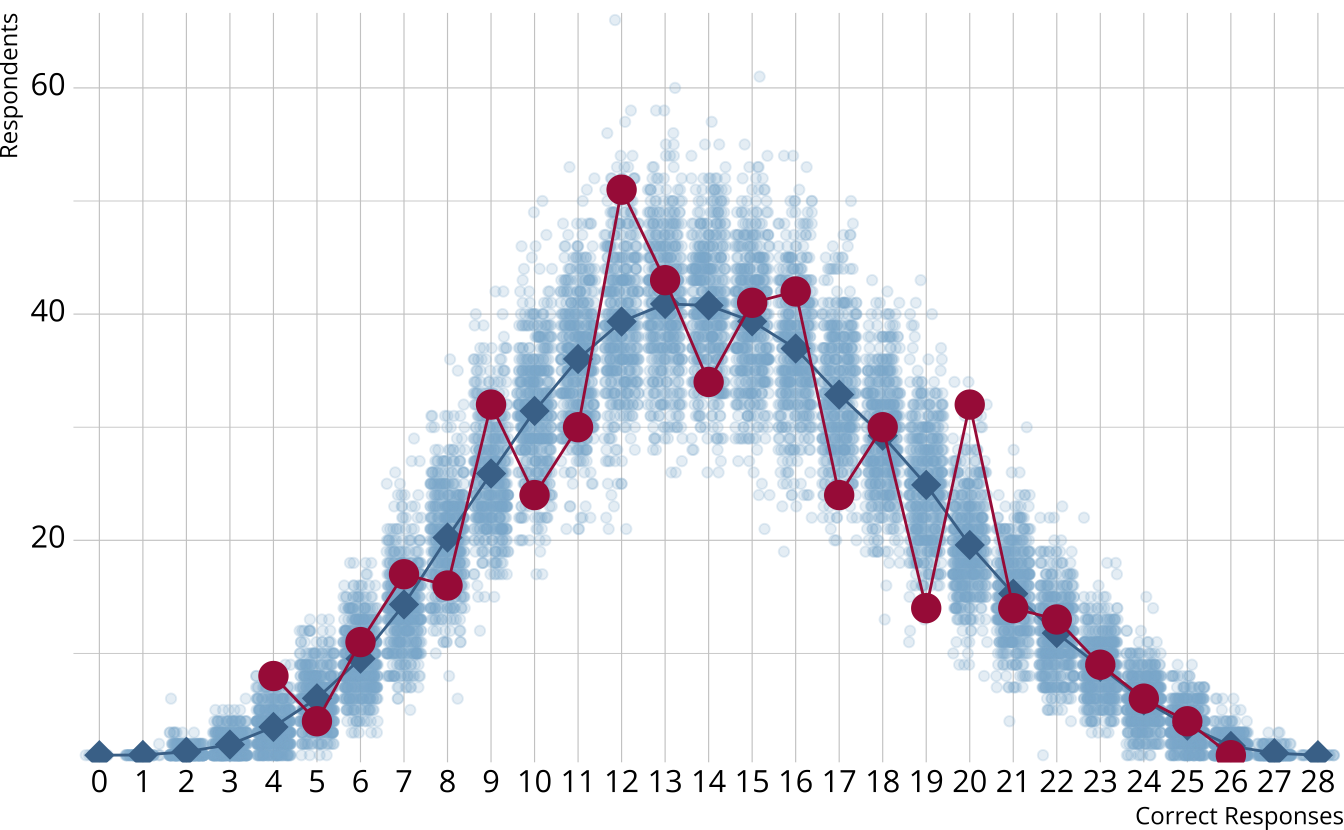
PPMC: χ2
- Calculate a χ2-like statistic comparing the number of respondents at each score point in each iteration to the expectation
- Calculate the χ2 value comparing the observed data to the expectation
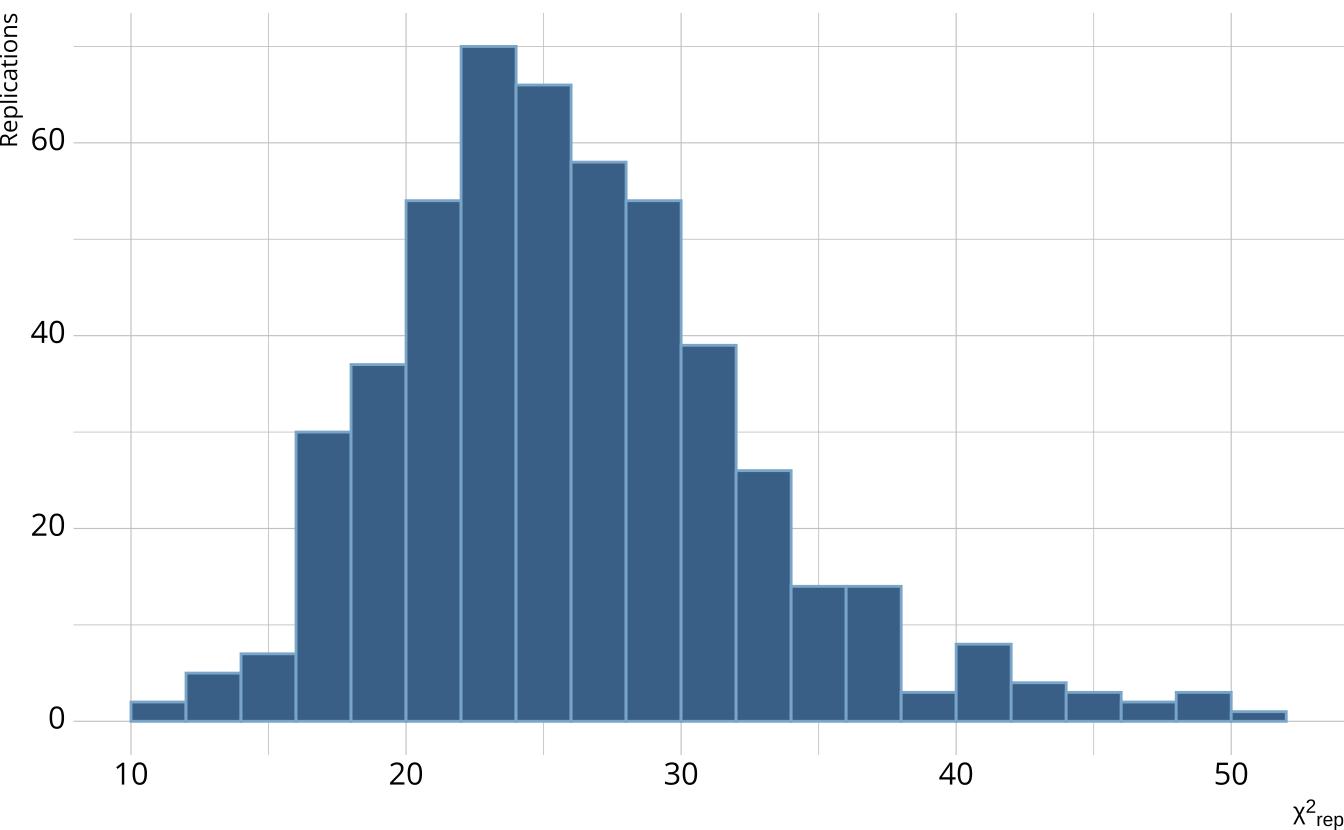
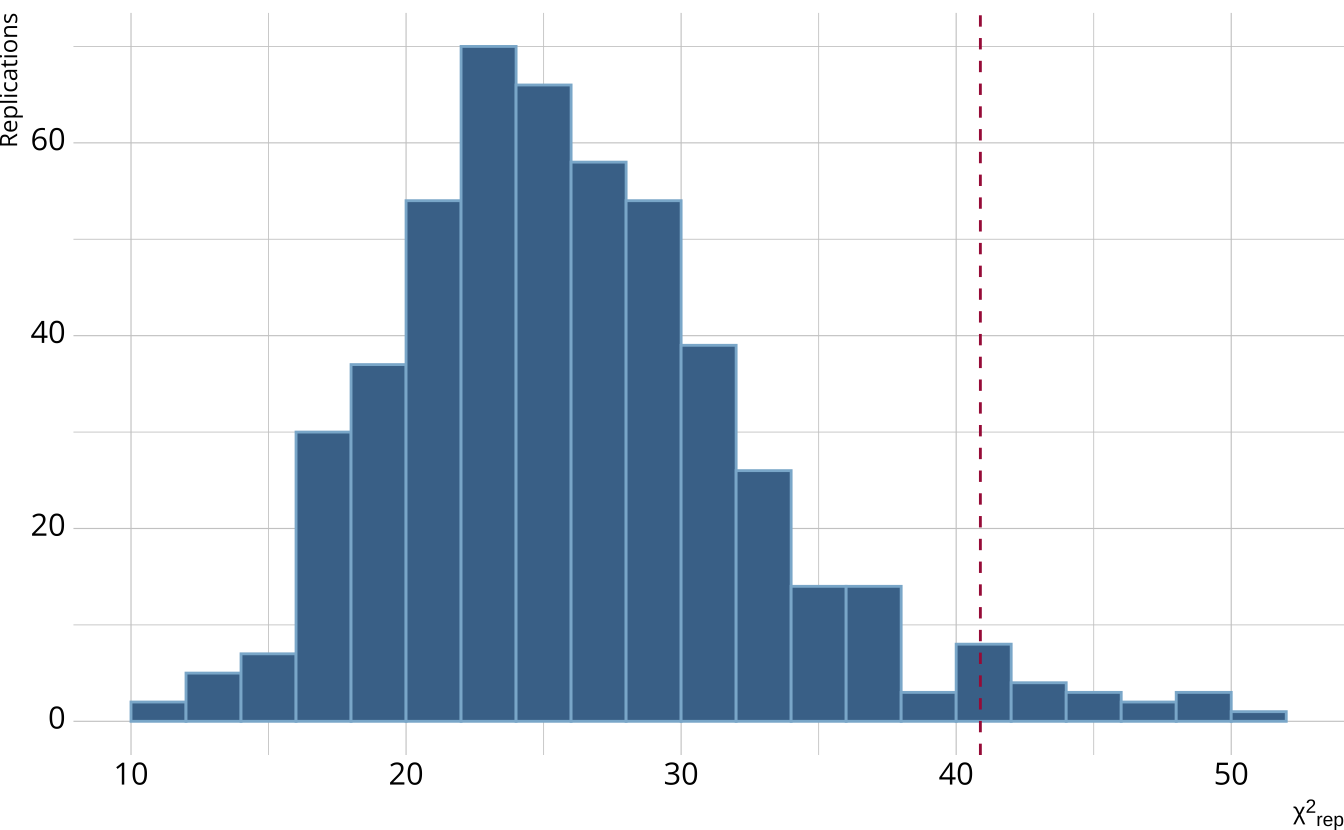
PPMC: ppp
- Calculate the proportion of iterations where the χ2-like statistic from replicated data set exceed the observed data statistic
- Posterior predictive p-value (ppp)
- ppp values between .025 and .975 represent acceptable model fit
# A tibble: 1 × 5
obs_chisq ppmc_mean `2.5%` `97.5%` ppp
<dbl> <dbl> <dbl> <dbl> <dbl>
1 35.9 30.7 14.9 57.1 0.207PPMC: Item-level fit
- We can also use PPMCs to calculate item-level statistics
- Conditional probabilities of classes providing a correct response
- Odds ratios between item pairs
# A tibble: 448 × 7
item class obs_cond_pval ppmc_mean `2.5%` `97.5%` ppp
<fct> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 [0,0,0,0] 0.162 0.207 0.135 0.274 0.894
2 1 [1,0,0,0] 0.609 0.629 0.537 0.714 0.668
3 1 [0,1,0,0] 0.429 0.320 0.243 0.409 0.01
4 1 [0,0,1,0] 0.332 0.207 0.135 0.274 0.0005
5 1 [0,0,0,1] 0.166 0.207 0.135 0.274 0.866
6 1 [1,1,0,0] 0.628 0.733 0.645 0.821 0.992
7 1 [1,0,1,0] 0.759 0.629 0.537 0.714 0.0005
8 1 [1,0,0,1] 0.522 0.629 0.537 0.714 0.988
9 1 [0,1,1,0] 0.277 0.320 0.243 0.409 0.847
10 1 [0,1,0,1] 0.298 0.320 0.243 0.409 0.679
# ℹ 438 more rows# A tibble: 378 × 7
item_1 item_2 obs_or ppmc_mean `2.5%` `97.5%` ppp
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 2 2.13 2.65 1.67 4.02 0.818
2 1 3 1.51 1.94 1.27 2.86 0.868
3 1 4 0.906 1.13 0.760 1.62 0.846
4 1 5 1.78 1.53 0.986 2.21 0.190
5 1 6 1.35 1.27 0.846 1.84 0.34
6 1 7 4.17 3.36 2.02 5.40 0.16
7 1 8 2.02 1.98 1.30 2.93 0.413
8 1 9 0.939 1.04 0.717 1.48 0.664
9 1 10 1.17 1.12 0.740 1.60 0.368
10 1 11 1.82 1.75 1.12 2.60 0.373
# ℹ 368 more rowsRelative fit
- Doesn’t give us information whether or not a model fits the data, only compares competing models to each other
- Should be evaluated in conjunction with absolute model fit
- Several options available for Bayesian models
- PSIS-LOO (Vehtari, 2017)
- WAIC (Watanabe, 2010)
Comparison model
- For a comparison, let’s estimate a DINA model to our same data set
- Reminder: DINA is a more restrictive model than the LCDM
Model comparison
- Calculate information criteria with
loo()orwaic() - Compare using
loo_compare() - If the absolute value of the difference is greater than 2.5 × standard error, that indicates a preference for the model in the first row
Reliability
Reporting reliability depends on how results are estimated and reported
Reliability for:
- Profile-level classification
- Attribute-level classification
- Attribute-level probability of proficiency
Profile-level classification
# A tibble: 500 × 17
album `[0,0,0,0]` `[1,0,0,0]` `[0,1,0,0]`
<fct> <rvar[1d]> <rvar[1d]> <rvar[1d]>
1 Melodrama 1.1e-06 ± 1.2e-06 1.3e-08 ± 1.4e-08 3.7e-05 ± 3.0e-05
2 A Night At The Oper… 9.5e-01 ± 2.3e-02 8.5e-03 ± 5.1e-03 8.5e-03 ± 5.3e-03
3 Cannibal (Expanded … 1.2e-02 ± 9.4e-03 4.2e-03 ± 3.4e-03 9.1e-01 ± 4.7e-02
4 BORN PINK 1.5e-01 ± 7.1e-02 1.6e-04 ± 1.2e-04 3.1e-01 ± 1.2e-01
5 Loose 8.5e-06 ± 9.6e-06 5.1e-08 ± 6.1e-08 1.5e-04 ± 1.2e-04
6 Red 1.8e-03 ± 1.9e-03 1.4e-02 ± 1.2e-02 9.7e-02 ± 6.2e-02
7 Wildfire 1.7e-04 ± 1.5e-04 1.6e-07 ± 1.7e-07 1.4e-03 ± 1.3e-03
8 Dawn FM 5.4e-05 ± 6.1e-05 2.6e-07 ± 2.8e-07 1.2e-03 ± 7.5e-04
9 thank u, next 7.1e-02 ± 4.9e-02 5.8e-06 ± 4.9e-06 3.7e-02 ± 2.5e-02
10 In A Perfect World … 1.2e-08 ± 1.6e-08 7.1e-05 ± 5.7e-05 9.8e-07 ± 8.7e-07
# ℹ 490 more rows
# ℹ 13 more variables: `[0,0,1,0]` <rvar[1d]>, `[0,0,0,1]` <rvar[1d]>,
# `[1,1,0,0]` <rvar[1d]>, `[1,0,1,0]` <rvar[1d]>, `[1,0,0,1]` <rvar[1d]>,
# `[0,1,1,0]` <rvar[1d]>, `[0,1,0,1]` <rvar[1d]>, `[0,0,1,1]` <rvar[1d]>,
# `[1,1,1,0]` <rvar[1d]>, `[1,1,0,1]` <rvar[1d]>, `[1,0,1,1]` <rvar[1d]>,
# `[0,1,1,1]` <rvar[1d]>, `[1,1,1,1]` <rvar[1d]># A tibble: 14 × 3
album profile prob
<fct> <chr> <dbl>
1 Red [1,0,1,0] 0.297
2 Fearless (Taylor's Version) [1,0,0,1] 0.869
3 Speak Now (Taylor's Version) [1,0,0,0] 0.351
4 Midnights [1,0,1,1] 0.831
5 reputation [1,0,1,0] 0.517
6 Red (Taylor's Version) [1,1,1,0] 0.488
7 Fearless [1,0,0,1] 0.523
8 1989 (Taylor's Version) [0,1,1,1] 0.797
9 Taylor Swift [0,0,0,1] 0.878
10 folklore [1,1,1,1] 0.979
11 Speak Now [1,0,0,0] 0.479
12 evermore [1,1,1,1] 0.704
13 Lover [0,0,1,1] 0.442
14 1989 [0,1,1,1] 0.797- Estimating classification consistency and accuracy for cognitive diagnostic assessment (Cui et al., 2012)
Attribute-level classification
# A tibble: 500 × 5
album songwriting production vocals
<fct> <rvar[1d]> <rvar[1d]> <rvar[1d]>
1 Melodrama 0.000419 ± 0.000278 0.9422 ± 0.0340 0.966461 ± 0.019196
2 A Night At The Op… 0.008565 ± 0.005107 0.0086 ± 0.0053 0.033112 ± 0.019671
3 Cannibal (Expande… 0.080788 ± 0.044734 0.9842 ± 0.0114 0.000045 ± 0.000039
4 BORN PINK 0.000471 ± 0.000233 0.3845 ± 0.1307 0.508834 ± 0.137168
5 Loose 0.001590 ± 0.001057 0.8967 ± 0.0614 0.935788 ± 0.042500
6 Red 0.746107 ± 0.099693 0.6544 ± 0.1407 0.703408 ± 0.128450
7 Wildfire 0.000059 ± 0.000035 0.1359 ± 0.1027 0.951212 ± 0.028540
8 Dawn FM 0.000650 ± 0.000407 0.9544 ± 0.0313 0.003481 ± 0.003005
9 thank u, next 0.000020 ± 0.000010 0.2147 ± 0.0833 0.890630 ± 0.065815
10 In A Perfect Worl… 0.997949 ± 0.001355 0.9638 ± 0.0216 0.004456 ± 0.004106
# ℹ 490 more rows
# ℹ 1 more variable: cohesion <rvar[1d]># A tibble: 14 × 5
album songwriting production vocals cohesion
<fct> <int> <int> <int> <int>
1 Red 1 1 1 0
2 Fearless (Taylor's Version) 1 0 0 1
3 Speak Now (Taylor's Version) 1 0 0 0
4 Midnights 1 0 1 1
5 reputation 1 0 1 0
6 Red (Taylor's Version) 1 1 1 0
7 Fearless 1 0 0 1
8 1989 (Taylor's Version) 0 1 1 1
9 Taylor Swift 0 0 0 1
10 folklore 1 1 1 1
11 Speak Now 1 0 0 0
12 evermore 1 1 1 1
13 Lover 0 0 1 1
14 1989 0 1 1 1$accuracy
# A tibble: 4 × 8
attribute acc lambda_a kappa_a youden_a tetra_a tp_a tn_a
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 songwriting 0.973 0.944 0.399 0.946 0.996 0.971 0.975
2 production 0.900 0.800 0.784 0.800 0.951 0.901 0.899
3 vocals 0.927 0.848 0.849 0.855 0.974 0.933 0.922
4 cohesion 0.958 0.916 0.413 0.917 0.992 0.961 0.956
$consistency
# A tibble: 4 × 10
attribute consist lambda_c kappa_c youden_c tetra_c tp_c tn_c gammak
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 songwriting 0.949 0.895 0.944 0.898 0.987 0.947 0.951 0.958
2 production 0.823 0.644 0.800 0.646 0.849 0.824 0.822 0.855
3 vocals 0.865 0.724 0.853 0.730 0.912 0.862 0.868 0.891
4 cohesion 0.920 0.838 0.916 0.841 0.969 0.922 0.919 0.940
# ℹ 1 more variable: pc_prime <dbl>- Measures of agreement to assess attribute-level classification accuracy and consistency for cognitive diagnostic assessments (Johnson & Sinharay, 2018)
Attribute-level probabilities
# A tibble: 500 × 5
album songwriting production vocals
<fct> <rvar[1d]> <rvar[1d]> <rvar[1d]>
1 Melodrama 0.000419 ± 0.000278 0.9422 ± 0.0340 0.966461 ± 0.019196
2 A Night At The Op… 0.008565 ± 0.005107 0.0086 ± 0.0053 0.033112 ± 0.019671
3 Cannibal (Expande… 0.080788 ± 0.044734 0.9842 ± 0.0114 0.000045 ± 0.000039
4 BORN PINK 0.000471 ± 0.000233 0.3845 ± 0.1307 0.508834 ± 0.137168
5 Loose 0.001590 ± 0.001057 0.8967 ± 0.0614 0.935788 ± 0.042500
6 Red 0.746107 ± 0.099693 0.6544 ± 0.1407 0.703408 ± 0.128450
7 Wildfire 0.000059 ± 0.000035 0.1359 ± 0.1027 0.951212 ± 0.028540
8 Dawn FM 0.000650 ± 0.000407 0.9544 ± 0.0313 0.003481 ± 0.003005
9 thank u, next 0.000020 ± 0.000010 0.2147 ± 0.0833 0.890630 ± 0.065815
10 In A Perfect Worl… 0.997949 ± 0.001355 0.9638 ± 0.0216 0.004456 ± 0.004106
# ℹ 490 more rows
# ℹ 1 more variable: cohesion <rvar[1d]># A tibble: 4 × 5
attribute rho_pf rho_bs rho_i rho_tb
<chr> <dbl> <dbl> <dbl> <dbl>
1 songwriting 0.920 0.917 0.710 0.991
2 production 0.715 0.710 0.595 0.898
3 vocals 0.783 0.782 0.637 0.942
4 cohesion 0.880 0.880 0.692 0.982- The reliability of the posterior probability of skill attainment in diagnostic classification models (Johnson & Sinharay, 2020)
Summary
Diagnostic classification models
Confirmatory latent class models with categorical latent variables
Many benefits over traditional methods
- Fine-grained, multidimensional results
- Incorporates complex item structures
- High reliability with fewer items
Broad applicability in educational and psychological measurement
Learn more about DCMs
Learn more about measr
https://epsy896-dcm.wjakethompson.com
Diagnostic Psychometrics